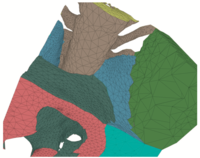
We propose a new strategy for boundary conforming meshing that decouples the problem of building tetrahedra of proper size and shape from the problem of conforming to complex, non-manifold boundaries. This approach is motivated by the observation that while several methods exist for adaptive tetrahedral meshing, they typically have difficulty at geometric boundaries. The proposed strategy avoids this conflict by extracting the boundary conforming constraint into a secondary step. We first build a background mesh having a desired set of tetrahedral properties, and then use a generalized stenciling method to divide, or 'cleave', these elements to get a set of conforming tetrahedra, while limiting the impacts cleaving has on element quality. In developing this new framework, we make several technical contributions including a new method for building graded tetrahedral meshes as well as a generalization of the isosurface stuffing and lattice cleaving algorithms to unstructured background meshes.