Edge Maps: Representing Flow with Bounded Error
|
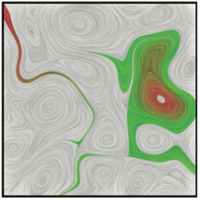
Robust analysis of vector fields has been established as an important tool for deriving insights from the complex systems these fields model. Many analysis techniques rely on computing streamlines, a task often hampered by numerical instabilities. Approaches that ignore the resulting errors can lead to inconsistencies that may produce unreliable visualizations and ultimately prevent in-depth analysis. We propose a new representation for vector fields on surfaces that replaces numerical integration through triangles with linear maps defined on its boundary. This representation, called edge maps, is equivalent to computing all possible streamlines at a user defined error threshold. In spite of this error, all the streamlines computed using edge maps will be pairwise disjoint. Furthermore, our representation stores the error explicitly, and thus can be used to produce more informative visualizations. Given a piecewise-linear interpolated vector field, a recent result [15] shows that there are only 23 possible map classes for a triangle, permitting a concise description of flow behaviors. This work describes the details of computing edge maps, provides techniques to quantify and refine edge map error, and gives qualitative and visual comparisons to more traditional techniques. |
[DOI/EE link]
@inproceedings{BJBCLNP11,
address = {Hong Kong, China},
author = {Harsh Bhatia and Shreeraj Jadhav and Peer-Timo Bremer and Guoning Chen and Joshua A. Levine and Luis Gustavo Nonato and Valerio Pascucci},
booktitle = {4th Pacific Visualization Symposium},
ee = {http://dx.doi.org/10.1109/PACIFICVIS.2011.5742375},
month = {3},
note = {Best Paper Award},
pages = {75--82},
publisher = {IEEE},
title = {Edge Maps: Representing Flow with Bounded Error},
year = {2011}
}